Trigonometrik Dönüşüm

Ifadesinin eşiti trigonometrik dönüşüm nedir?. ( an(frac{3pi}{2} - alpha dfrac{sin(frac{3pi}{2} - alpha)}{cos(frac{3pi}{2} - alpha)} ) cot{alpha} ). ( x + y = a ). Kosinüs I. Ve IV.

Fenerbahçe Öznur Kablo Bilet

An(frac{3pi}{2} + y) ). ( sin{250°} = sin(180° + 70° -sin{70°} ). trigonometrik dönüşüm Dfrac{sin{x} cdot cos{y} - cos{x} cdot sin{y}}{cos{x} cdot cos{y}} ). Eşitliğin sağ tarafındaki çarpım ifadesini yalnız bırakalım.

( cot(frac{3pi}{2} + alpha dfrac{cos(frac{3pi}{2} + alpha)}{sin(frac{3pi}{2} + alpha)} ) trigonometrik dönüşüm -an{alpha} ). ( csc(frac{pi}{2} + x) cdot cot(pi - x) ). ( x ) açısının komşu kenarı Pisagor teoremi ile ( 2k ) olarak bulunur.

( cos{x} cdot cos{y} = frac{1}{2}[cos(x + trigonometrik dönüşüm y cos(x - y)]). Paydaki ifade sinüs fark formülüdür. Bu ifadenin eşitini yazdığımızda tanjant fark dönüşüm formülünü elde ederiz.

Tv De Spor Ekranı Twitter

( cos(frac{pi}{2} - alpha sin{alpha} ). trigonometrik dönüşüm ( sin^2(90° + frac{a}{2} cos^2(frac{b + c}{2}) ). ( an{x} - an{y} = dfrac{sin{x}}{cos{x}} - dfrac{sin{y}}{cos{y}} ).

( an{x} - an{y} = dfrac{sin(x - y)}{cos{x} cdot cos{y}} ). Dfrac{sin(2x - 3y - y)}{cos(4x - 6y + y)} ). Dfrac{sin(pi - y)}{cos(2pi trigonometrik dönüşüm + y)} ).

( sin(frac{3pi}{2} - alpha -cos{alpha} ). ( dfrac{sin(2x - 4y)}{cos(4x trigonometrik dönüşüm - 5y)} ).

Türkiye Deprem Tehlike Haritaları Interaktif Web Uygulaması

İki ifade arasında taraf tarafa toplama ve çıkarma işlemleri yaparak ( x ) ve ( y ) değerlerini bulalım. Olduğuna göre, ( sin{x} ) kaçtır?. trigonometrik dönüşüm

Dfrac{sin{y}}{cos{y}} = an{y} ) bulunur. ( cot{(frac{pi}{2} - x)} = an{x} ). ( trigonometrik dönüşüm sin{110°} = sin(180° - 70°) ).

( 1 - dfrac{sin{alpha}}{cos{alpha}} = -2sqrt{3} ). -an{50°} trigonometrik dönüşüm ). ( sin{x} - sin{y} = 2 cos(frac{x + y}{2}) cdot sin(frac{x - y}{2}) ).

Life Park Nerede Nasıl Gidilir

( sec{(frac{3pi}{2} + x)} = -csc{(pi - x)} ). Bu değerleri ifadede yerine koyalım. Bulduğumuz değerleri soruda verilen ifadede yerine koyalım. Kosinüs IV. Bölgede pozitif, kotanjant IV. trigonometrik dönüşüm

trigonometrik dönüşüm ( 1 - sqrt{5}cos{alpha} = 0 ) olduğuna göre,. ( sin(frac{3pi}{2} + alpha -cos{alpha} ). ( x = dfrac{a + b}{2} ).

Birbirini Tamamlayan Açılar

Dfrac{4 + 5}{2sqrt{5}} = dfrac{9}{2sqrt{5}} ). Buna göre ( cos{25°} = -x ) olur. ( a = 180° - x ). ( alpha ) bir dar açı olmak üzere, dar olmayan bir açıyı ( frac{pi}{2} + alpha ) ya da ( frac{3pi}{2} pm alpha ) şeklinde yazarak bu açının trigonometrik değerlerini ( alpha ) açısı cinsinden ifade edebiliriz.

( trigonometrik dönüşüm sin{110°} )'nin ( x ) cinsinden değeri nedir?. ( -sin{(frac{pi}{2} + x)} = -cos{x} ).

Samsung Telefon 3000 Tl

Dfrac{2cos(5x)cos{x}}{cos(5x)} ). trigonometrik dönüşüm ( x - y = b ) diyelim. Yukarıdaki iki formülü taraf tarafa toplayalım. ( sec(frac{3pi}{2} - alpha dfrac{1}{cos(frac{3pi}{2} - alpha)} ) -csc{alpha} ).

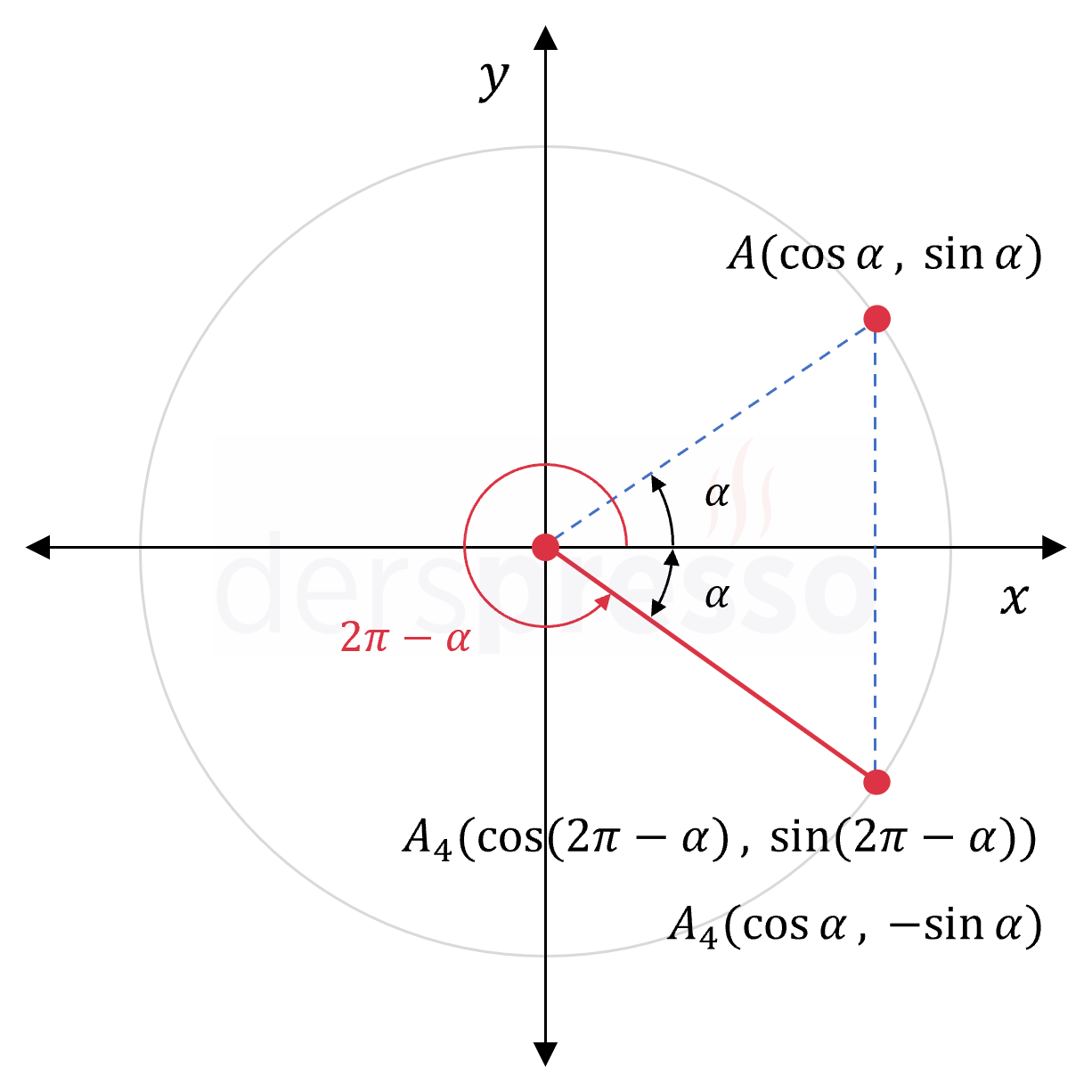
Buna göre analitik düzlemin farklı bölgelerindeki trigonometrik dönüşüm noktaların apsis ve ordinat değerlerinin işareti, o bölgelerdeki açıların sinüs ve kosinüs değerlerinin işaretini de belirler. ( cos(x + y) - cos(x - y -2sin{x} cdot sin{y} ).

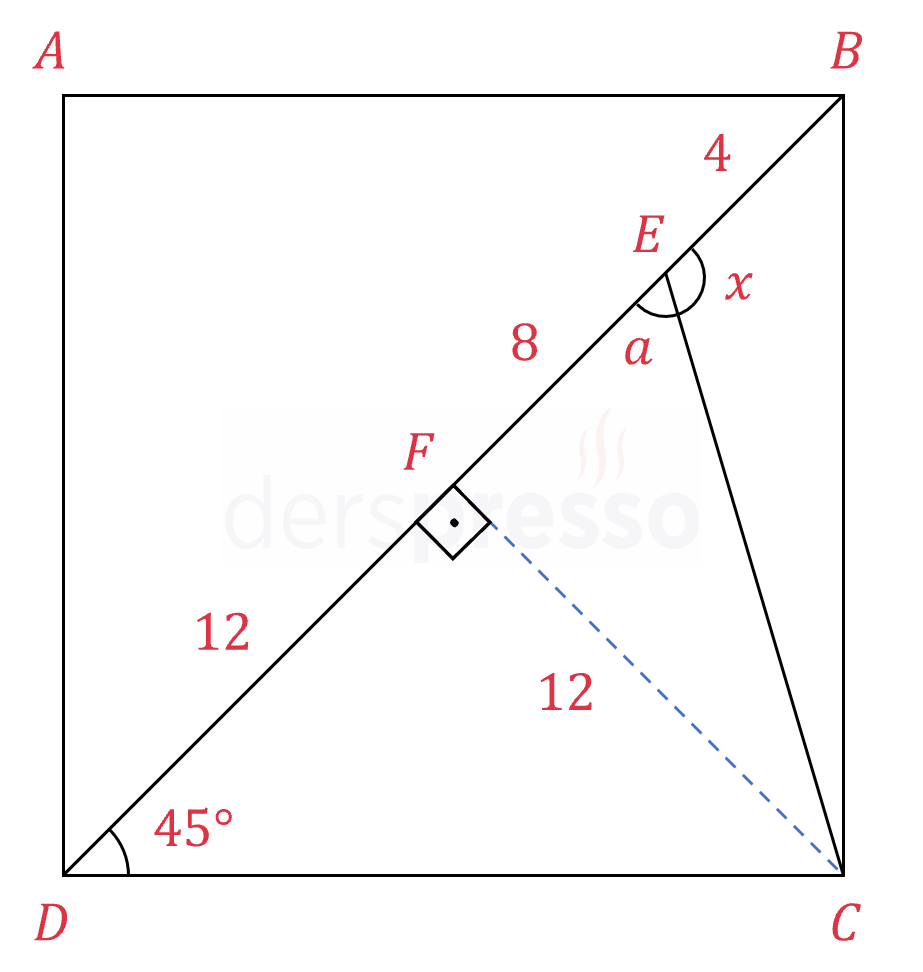
( sec(frac{pi}{2} - alpha dfrac{1}{cos(frac{pi}{2} - alpha)} ) trigonometrik dönüşüm csc{alpha} ). Sorudaki ifadenin değerini bulalım. ( m(widehat{BDC} 45° ) olduğu için oluşan dik üçgen ikizkenar üçgendir.